Proving a Beautiful Identity in Dafny

Recently, I came across a tweet about the following identity:

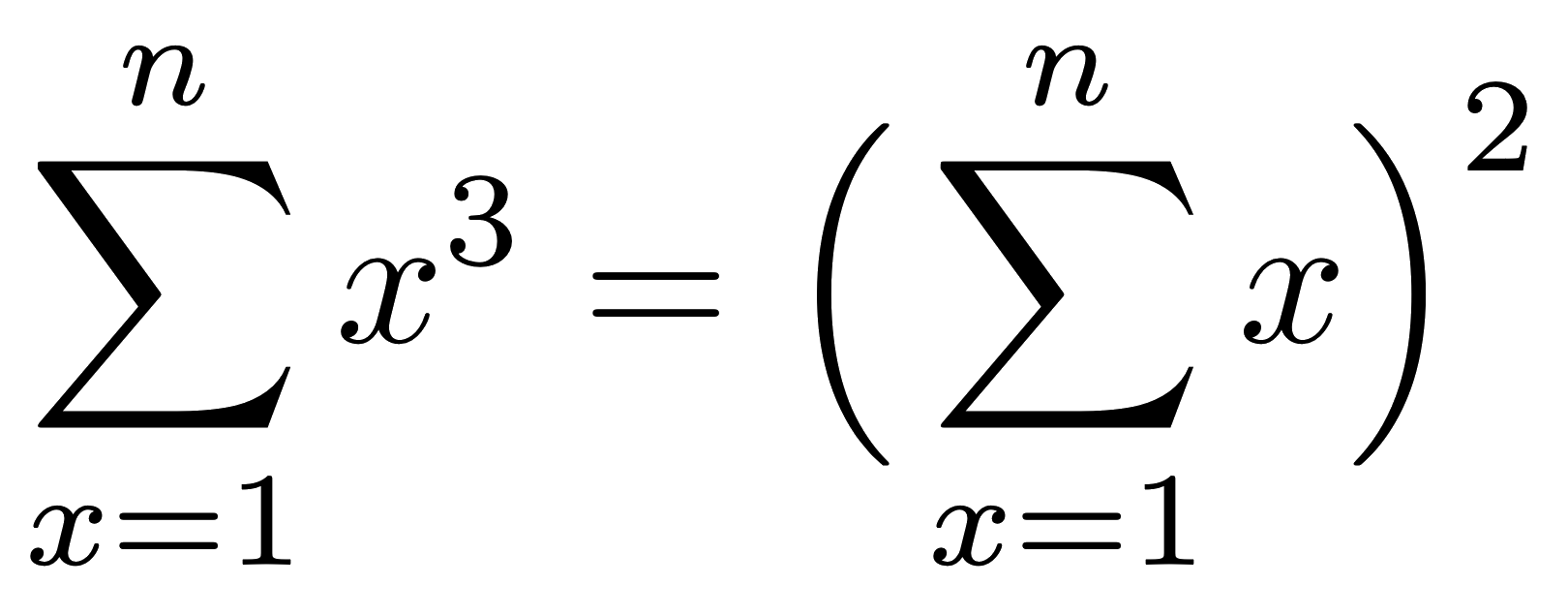
This seemed quite surprising to me, though the tweet’s thread included a number of proofs. We can check the first few values easily for ourself:

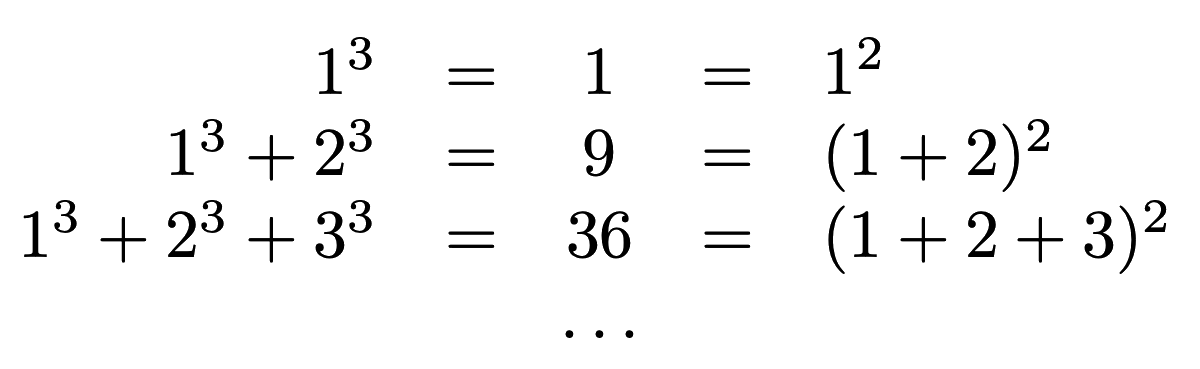
So, the thought occurred: can we prove this identity with Dafny?

Setup

Before we can prove the identity we need to first translate it into Dafny. This is actually pretty straightforward, and we can translate the left-hand side of our identity as follows:

function Sum3(n:nat) : nat 
requires n > 0 {
  if n == 1 then 1 
  else 
     Sum3(n-1) + (n*n*n)
}

This describes the sum of cubes using a recursive function, which works out well. For the right-hand side, we’ll use the following:

function Sum(n:nat) : nat 
requires n > 0 {
  if n == 1 then 1
  else 
    Sum(n-1) + n
}

This describes the sum from 1 to n, which can then be squared. We can now express the identity as follows:

lemma Identity(n:nat) 
requires n > 0 
ensures Sum(n) * Sum(n) == Sum3(n) 
{
   ...
}

Here, the precondition n > 0 is required for both Sum(n) and Sum3(n) to make sense. Furthermore, the ... is where our proof goes (more on this below).

Proof

At this point, I’ll jump right in and show the Dafny proof:

lemma Identity(n:nat) 
requires n > 0 
ensures Sum(n) * Sum(n) == Sum3(n) 
{
  if n != 1 {
    var m := n-1;
    assert Sum(n)*Sum(n) == Sum(m)*Sum(m) + n*n*n;	
    assert Sum3(n) == Sum(m)*Sum(m) + n*n*n;
} }

This proof probably seems quite strange (certainly, it does to me) so let’s unpack it. First, it’s worth noting that I did not just write this out first time and get it. In fact, I spent several hours playing around with various intermediate forms before finally arriving at what we have above. Specifically, it took me a while to realise Sum(n)*Sum(n) == Sum(m)*Sum(m) + n*n*n which was key (I actually didn’t look at the existing proofs beforehand, so I was starting out from scratch).

Anyway, hopefully it is reasonably clear that, if both assertions above hold, then the final identity holds. So the proof really breaks down into two parts, one for each assertion.

First Assertion

The first assertion claims the following holds (where m==n-1 as above):

Sum(n)*Sum(n) == Sum(m)*Sum(m) + n*n*n

We can actually see this holds reasonably easily for ourselves. First, start out with the equivalence:

Sum(n)*Sum(n) == Sum(n)*Sum(n) 

Then, unroll Sum() once on the right-hand side to get:

Sum(n)*Sum(n) == (Sum(m)+n)*(Sum(m)+n)

Next, multiply out the right-hand side to give:

Sum(n)*Sum(n) == Sum(m)*Sum(m) + 2*n*Sum(m) + n*n

Finally, apply the well-known equivalence to get Sum(m) = m*(m+1)/2. Since m==n-1, this is actually Sum(m) == m*n / 2. Now, substituting this into the middle term of our equation and simplify:

Sum(n)*Sum(n) == Sum(m)*Sum(m) + n*n*n

And, at this point, we’re done! What’s impressive is that Dafny appears to do all of this for us (more on this later).

Second Assertion

The second assertion claims the following holds:

Sum3(n) == Sum(m)*Sum(m) + n*n*n

This is relatively easy to arrive at by induction. When n > 0 then Sum(m)*Sum(m) == Sum3(m) by induction. Thus, start out with:

Sum3(n) == Sum3(n)

Then, unrolling Sum3(n) on the right-hand side gives:

Sum3(n) == Sum3(m) + n*n*n

And, at this point, apply the inductive hypothesis:

Sum3(n) == Sum(m)*Sum(m) + n*n*n

Finally, its worth noting that Dafny automatically applies induction for us (when it can). Hence, it was able to show this second assertion without further help.

Manual Induction

The original Dafny proof above relies heavily on Dafny’s automatic induction. So, I thought it would be interesting to develop a proof without relying on this. This is what I ended up with:

lemma {:induction false} Identity(n:nat) 
requires n > 0 
ensures Sum(n) * Sum(n) == Sum3(n) 
{
  if n != 1 {
    var m := n-1;
    Identiy(m); // apply induction
    calc {
      Sum(n)*Sum(n);
    ==
      Sum(m)*Sum(m) + 2*n*Sum(m) + n*n;
    == { Sum1toN(m); }
      Sum(m)*Sum(m) + 2*n*((n*m)/2) + n*n;
    == { NNm1Mod2(n); }
      Sum(m)*Sum(m) + n*(n*m) + n*n;
    == 
      Sum(m)*Sum(m) + n*n*n;
} } }

Here, {:induction false} turns off Dafny’s automatic induction. Also, Dafny’s calc statement walks us through the intermediate steps required to establish the first assertion above. The curious thing, however, is that I needed the following intermediate lemmas:

lemma Sum1toN(n:nat) 
requires n > 0 
ensures n * (n + 1) / 2 == Sum(n) {}

lemma NNm1Mod2(n:nat) 
requires n > 0
ensures (n*(n-1)) % 2 == 0 {
  if n%2 == 0 { Mod2(n,n-1); } 
  else {
    Mod2(n-1,n);
    assert ((n-1)*n) % 2 == 0;
} }

lemma Mod2(n:nat,m:nat) 
requires n%2 == 0
ensures (n*m) % 2 == 0 {
  if m > 0 { Mod2(n,m-1); }
}

This is curious because I’m unclear how Dafny proved the original version of the proof without these Lemma’s. Its possible there is an easier proof via manual induction which I didn’t find.

Conclusion

If you’ve made it this far, then well done! In the end, it was a fair amount of work to prove the original identity in Dafny. Still, I find it pretty amazing that I could prove it from scratch without too much trouble.