Type Checking in Whiley goes Both Ways!

Type checking in Whiley is a curious thing as it goes both forwards and backwards. This is sometimes referred to as bidirectional type checking (see e.g. here and here). This is surprisingly useful in Whiley (perhaps because the language has a reasonably unusual feature set).

Backwards Typing

Type checkers normally work in a backwards (or bottom up) direction. That is, they start from leaves of the abstract syntax tree and work upwards. Typing a statement like xs[i] = ys[i] + 1 (when xs and ys have type int[]) might look something like this:

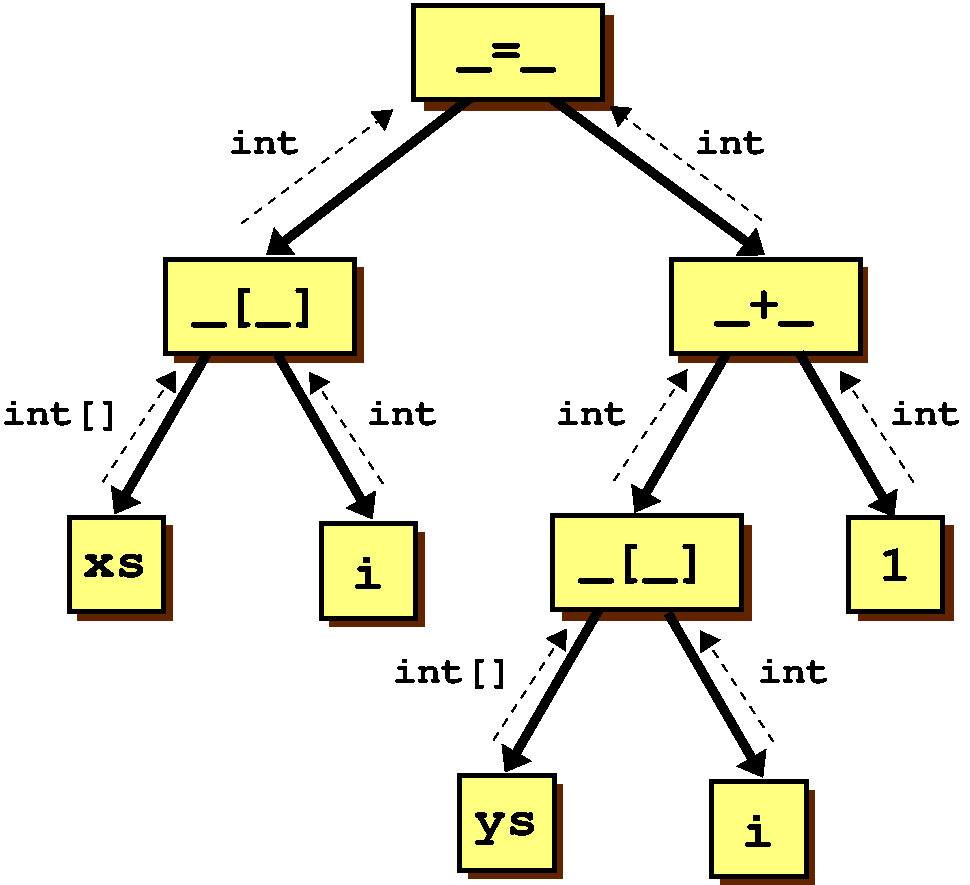
They key here is that types have to agree (modulo subtyping), otherwise we have a type error.

Limitations

As a general approach, backwards typing works well in most cases. But, there are some limitations when applying this to Whiley:

• (Sizing). Variables of type int in Whiley can hold arbitrary sized integers and, because of this, backwards typing can lead to inefficiency. Consider this:

  u8 x = 124
  

  Under the backwards typing scheme, the constant 124 is given type int. That means, under-the-hood when the constant is created, we’ll allocate space for an arbitrary sized integer and give it the value 124. Then, we’ll immediately coerce it to a u8 causing a deallocation. It would be much better if we automatically determined the type of 124 was u8 rather than int. Note, one way to solve this is with specific notation for constants (e.g. 124u8 in Rust) — however, bidirectional typing is more elegant.

• (Overloading). Whiley, like many languages, provides the ability to overload functions. Backwards typing supports this on parameter types but not on return types. Whilst it may seem esoteric, the ability to overload on return types can be useful. For example, you might want to do something analoguous to the default trait in Rust:

  function default() -> int[]:
     return []
  
  function default() -> int:
     return 0
  

  This is valid Whiley and, with bidirectional typing, the compiler can automatically select the right method based on context.

• (Templates). Inferring template parameters saves tedious effort writing them out, and results in more elegant code. In many cases, backwards typing can be used for inferring parameters — but there cases where it doesn’t work. The following is based on a real-world situation involving the Web.wy library:

  ...
  type Element<T> is { 
     string name, 
     Attribute<T>[] attributes,
     Node<S>[] children
  }
  type Node<T> is Element<T> | string
  
  function h1<T>(Node<T> child) -> Element<T>:
     ...
  

  The intention here is to allow an HTML heading to be created with something like h1("Title"). Earlier versions of Whiley (which only used backwards typing) could not infer a type for T and, instead, required you to provide this explicitly (which was cumbersome). The problem is that the supplied parameter "Title" provides no suitable binding for T. Fortunately, with bidirectional typing, Whiley can now infer the type of T based on what the result is being assigned to.

Forwards Typing

A key observation is that, in many situations, we already have concrete type information available. For example, consider this declaration:

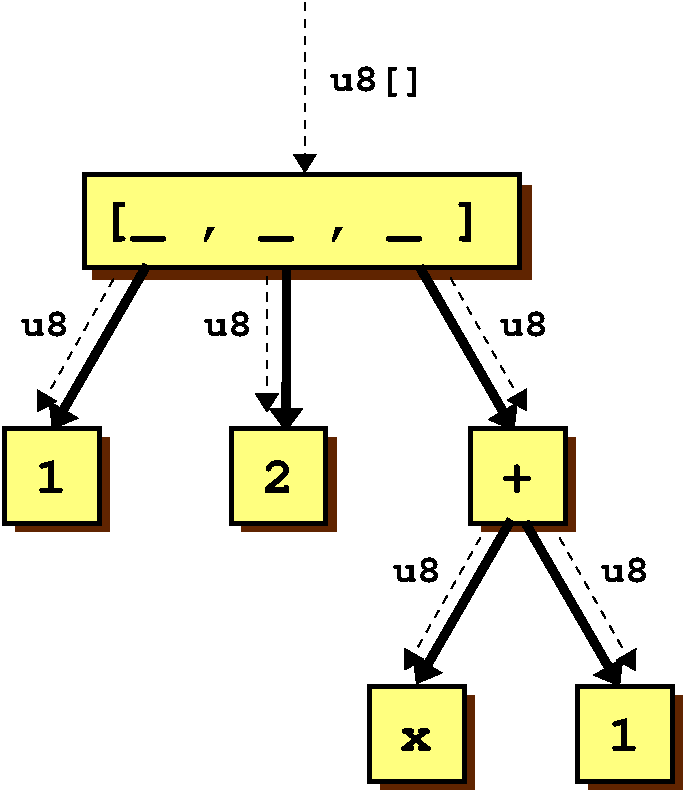
u8[] bytes = [1,2,3]

We can type this in a forwards (or top down) direction by “pushing down” from the declared type u8[] of bytes. This means we give [1,2,x+1] the type u8[] and then push u8 into each of the subexpressions 1, 2, and x+1, as follows:

Bidirectional Typing

Bidirectional typing, as the name suggests, is about mixing forwards and backwards typing. But, you might wonder why we don’t just use forwards typing all the time? Well, the answer is pretty simple: in some cases, you simply cannot use forward typing. Therefore, in such cases, we default back to backwards typing. The following illustrates such an example:

function headerOf<T>(Node<T> n, Node<T> c) -> bool:
  return n == h1(c)

The issue is that the type being pushed down from the return statement into its expression is bool, but this provides no useful information about the operand types for ==. In otherwords, when typing n we simply don’t have a type to push down. What we can do instead, however, is “pull up” the type from n and then push that down into h1(c).

In the example above, there wasn’t a type we could push down into the subexpression. So, we didn’t have any choice but to pull up instead. However, there are situations where we have a type to push down — but it is undesirable to do so. The following illustrates:

u8[] items = [0,1,2]
u16 item = items[0]

In the above, we can push u16 into items[0] and, based on this, push u16[] into down into the access of items. However, this then forces a coercion of the entire items array from u8[] to u16[]. This is less than ideal since we only want to access (and, hence, coerce) one element from items. Therefore, when typing items[0] its preferable to pull the type of items up (as this corresponds to its natural representation). This then forces a coercion from u8 to u16 at that point, rather than further down the tree.

Conclusion

Bidirectional typing allows for more concise and elegant code than the typical bottom up approach. This has considerably improved the user experience when writing Whiley code. However, it is worth noting that bidirectional type checking algorithm now used in Whiley is considerably more involved than the original bottum up algorithm.

References

A few useful papers on the subject:

• Bidirectional Typing, J. Dunfield and N. Krishnaswami. In ACM Computing Surveys, 2021. PDF

• Complete and Easy Bidirectional Typechecking for Higher-Rank Polymorphism, J. Dunfield and N. Krishnaswami. In ICFP, 2013. PDF