Test-Driving the Rust Model Checker (RMC)

The Rust Model Checker (RMC) allows Rust programs to be model checked using the C Bounded Model Checker (CBMC). In essence, RMC is an extension to the Rust compiler which converts Rust’s MIR into the input language of CBMC (GOTO).

Using RMC provide can provide much stronger guarantees than, for example, testing with cargo-fuzz or proptest. To understand how it works, I’m going to walk through the process of checking the following simple function:

fn index_of(items: &[u32], item: u32) -> usize {
    for i in 0..items.len() {
        if items[i] == item {
            return i;
        }
    }
    //
    return usize::MAX;
}

This is a good function for testing verification systems, since it has some nice post-conditions. To get started we need to add some helper methods, the first of which is:

fn __nondet<T>() -> T { 
   unimplemented!() 
}

This function is known to RMC and has special significance. Here, __nondet<T>() returns a non-deterministic value. We can think of this as an arbitrary value of the type T in question. This is where the power of RMC comes from as, instead of testing individual values of T, we’re testing all possible values of T! The second helper method we need is this:

fn __VERIFIER_assume(cond: bool) { 
   unimplemented!() 
}

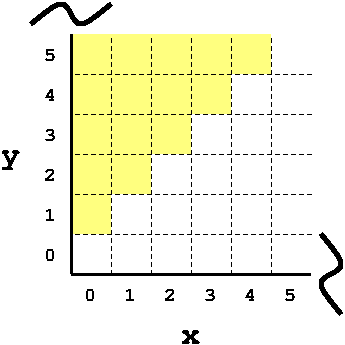
Again this has specifical significance to RMC and, as we’ll see, it is used for constraining non-determinstic values. For example, we might do something like this:

let x : u32 = __nondet();
let y : u32 = __nondet();
__VERIFIER_assume(x < y);

Here, we assigned arbitrary values to x and y and then constrained x so that its always below y. Perhaps we had to do this to meet some requirement of the API we’re testing. This means RMC will never consider the values e.g. x=10, y=10 or x=255, y=0. But, it will still consider all values where x < y, such as x=0,y=1, x=255,y=256, etc. We can visualise this as follows:

Our First Proof

We’re now going to write our first “test” using RMC. Except that its not a test in the conventional sense, since we’re using arbitrary values. To try and make this distinction clear, RMC instead refers to them as proofs.

So, let’s write our first proof:

#[cfg(rmc)]
#[no_mangle]
pub fn test_01() {
  let xs : [u32; 2] = __nondet();
  assert!(index_of(&xs,0) == usize::MAX);
}

This tells RMC to test index_of() for all possible arrays of size 2. We can run RMC using e.g. rmc index_of.rs (if that’s the name of our file) and, in doing this, RMC will find the assert can fail. This makes sense as some arrays may contain 0 so index_of() will not always return usize::MAX. This is the key difference between using RMC and an automated testing tool: upto certain bounds, RMC checks all possible values.

NOTE: At the moment, RMC requires #[cfg(rmc)] to identify proofs. However, the plan is eventually to use #[proof] in the same way #[test] is used.

Anyway, something isn’t quite right yet. The index_of() method is correct, but our proof is failing. We need to refine our proof so that it reflects the true contract of index_of(). Specifically, when given an array xs which doesn’t contain 0, we expect index_of(xs,0) to return usize::MAX. The question is how to set this up with RMC. In fact, it’s pretty easy since we know the size of xs:

#[cfg(rmc)]
#[no_mangle]
pub fn test_01() {
  let xs : [u32; 2] = __nondet();
  __VERIFIER_assume(xs[0] != 0);
  __VERIFIER_assume(xs[1] != 0);
  assert!(index_of(&xs,0) == usize::MAX);
}

We’ve used __VERIFIER_assume() to tell RMC that it should assume the elements in our array do not hold 0. And finally RMC now reports, as expected, that our proof suceeds!

Going Forward

So, we’ve written our first proof. Now what? Well, since our proof only applies for arrays of size 2, it would be nice to generalise it. Unfortunately, testing arrays of arbitrary size is beyond the limit of RMC but, for example, we can prove all arrays upto size 3. Furthermore our proof only checked for item=0 but it would be better to check for arbitrary values. So, let’s put that altogether:

#[cfg(rmc)]
#[no_mangle]
pub fn test_01() {
  let x : u32 = __nondet();
  let len : usize = __nondet();
  let xs : [u32; 3] = __nondet();  
  // Apply Constraints  
  __VERIFIER_assume(len <= 3);
  __VERIFIER_assume(xs[0] != x);
  __VERIFIER_assume(xs[1] != x);
  __VERIFIER_assume(xs[2] != x);
  // Check
  assert!(index_of(&xs[..len],x) == usize::MAX);
}

This is getting more interesting! Now we’re looking for an arbitrary value x instead of 0. Likewise, the final statement takes a slice of xs upto a given length len. Since len is constrained to be anything upto and including length 3, this means RMC now checks all arrays upto length 3.

Our updated proof represents a significant improvement over the first. But, there are still tweaks we can make. For example, it’s good to employ a constant LIMIT which determines the maximum length:

  ...
  let xs : [u32; LIMIT] = __nondet();
  // Ensure length at most LIMIT
  __VERIFIER_assume(len <= LIMIT); 
  // Ensure element not in array below len
  for i in 0..len {
    __VERIFIER_assume(xs[i] != x);
  }  
  ...

Using LIMIT means we can easily try larger maximum lengths to see how far RMC can go. However, using a for loop does cause some difficulties for the underlying CBMC tool. To resolve this, we must provide a command-line argument --unwind X where X is some bound (e.g. 3). This tells CBMC to unroll the loop at most X times. In this case the maximum length of the array determines (roughly speaking) how much unrolling CBMC needs to be confident the proof holds.

The Flip Side

Now we’ve generalised our proof, its looking pretty nice. But, it only checks the case when item is not in items — that’s only half the story! So, we should add a second proof for the case where item is in items. This is my first attempt:

#[cfg(rmc)]
#[no_mangle]
pub fn test_02() {
    let x : u32 = __nondet();
    let len : usize = __nondet();
    let xs : [u32; LIMIT] = __nondet();    
    let i : usize = __nondet();
    // Apply Constraints
    __VERIFIER_assume(len <= LIMIT);
    __VERIFIER_assume(i < len);
    __VERIFIER_assume(xs[i] == x);    
    // Compute result
    let result = index_of(&xs[..len],x);
    // Check it matches
    assert!(xs[result] == x);
}

This is roughly similar to before, except we now require some i where xs[i] == x. Also, we cannot assume index_of(&xs[..len],x) returns i since there might be more than one occurence of x in the array.

We can observe that index_of() actually returns the first index of item. So, to make things more interesting, let’s assume this is actually part of its contract. To check this, we must further constrain xs to ensure x does not occur below i as follows:

  ...
  // Ensure nothing below i matches
  for j in 0..i {
    __VERIFIER_assume(xs[j] != x);
  }
  // Check found correct one
  assert!(index_of(&xs[..len],x) == i);
  ...

From this we see that RMC proofs can be made quite sophisticated using just the __nondet<T>() and __VERIFIER_assume() statements. Also, its worth noting another way of achieving this is to do the check after calling index_of() (thanks to @zhassan-aws for pointing this out):

  ...
  let result = indexof(&xs[..len],x);
  // Check it matches
  assert!(xs[result] == x);
  // Check its first
  for j in 0..result {
     assert!(xs[j] != x);
  }
  ...

Conclusion

Hopefully this has given you an insight into how RMC works, and what a proof is like. We’ve only touched the tip of the iceberg here, but the post was already quite long! You can learn more about using RMC from the Getting Started Guide. Also, I found this paper provides good background on using tools like this in an industrial setting.

Finally, if you want to play around with RMC, here are a few suggestions of things you could try:

• Implement fill(items: &mut [u32], item: u32) which fills a given array items with a given value item.

• Implement reverse(items: &mut [u32]) which reverses the contents of items.

• Implement index_of() using Vec<T> instead of a slice.