Dynamic Cycle Detection for Lock Ordering

Recently, I discovered that an algorithm of mine from a few years back is being used in both TensorFlow and the Abseil C++ library (see here and here). That is of course pretty exciting since they are both widely used libraries! So, I thought it would be interesting to look at what it is being used for.

Deadlock Detection

In Abseil, the algorithm is used in mutex to ensure locks are acquired in a consistent order. Suppose we have two mutexes M0 and M1 which can be held at the same time by two threads. A deadlock can easily occur if, for example, the first thread acquires M0 then M1, whilst the second acquires M1 then M0. This doesn’t mean a deadlock will happen every time. But if, by chance, the first thread acquires M0 at the same time as the second aqcuires M1 — then we have a deadlock.

On the other hand, if mutexes are acquired according to a globally consistent ordering (e.g. M0 always acquired before M1), then no deadlock can arise. The challenge is to determine an appropriate ordering of mutexes. In fact, mutex does not attempt to determine this statically (presumably this is considered too hard). Instead, it simply observes program execution and reconstructs the ordering dynamically. Then, during execution, if some thread attempts to acquire a mutex in an order inconsistent with this, a potential deadlock is reported.

Acquires-Before Graph

To detect deadlocks, mutex maintains a (global) ordering of lock acquisitions called the aquires-before graph. This is implemented using a global variable called deadlock_graph which stores a directed acyclic graph, such as the following:

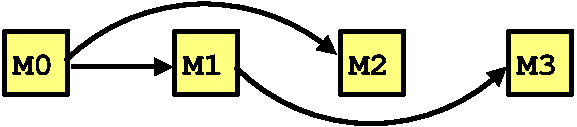
Here, we have four mutexes and an edge Mx -> My means Mx must be acquired before My. Actually, it indicates that Mx has been acquired before My in all lock acquisitions observed thus far. As an example, consider mutex M3. Both M0 and M1 must be acquired before M3. In contrast, it doesn’t matter whether M2 is acquired before M3 or not.

Mutexes which are unordered with respect to each other (as for M2 and M3 above) are ordered on demand. For example, if a thread comes along and acquires M2 whilst holding M3, the ordering is updated accordingly:

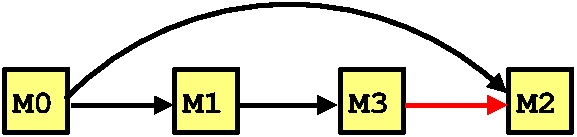
From now on, any attempt to acquire M2 before M3 generates an error message highlighting the potential deadlock. To make this work, every thread is associated with the mutexes it currently holds. When a thread holding mutex Mx attempts to acquire mutex My, the corresponding edge is added to deadlock_graph. If that edge introduces a cycle, we have a potential deadlock. Otherwise, the ordering is updated (as above) and execution proceeds.

At this point, it is becoming clear that performance is an issue. Whenever any thread acquires a lock, the deadlock_graph must be updated and the current ordering recalculated. For this reason, deadlock detection in mutex is only enabled when debugging. Furthermore, an efficient algorithm for updating the ordering is desirable (and this is where my algorithm comes in).

Dynamic Cycle Detection

Detecting cycles in a directed graph is actually pretty easy. We can just traverse the entire graph using a depth-first search and, if we encounter a vertex already visited, then we’ve found a cycle. We can also use Tarjan’s algorithm for detecting strongly connected components if we want to know what’s in the cycle.

Whilst detecting cycles is easy, the challenge lies in doing it efficiently after an edge has been inserted. A simple solution is just to retraverse the entire graph (e.g. using Tarjan’s algorithm), but this is quite wasteful. Instead, my algorithm limits the traveral as much as possible by maintaining a topoligical (i.e. consistent) ordering of the graph. For example, consider adding the edge M3 --> M1 to the following graph:

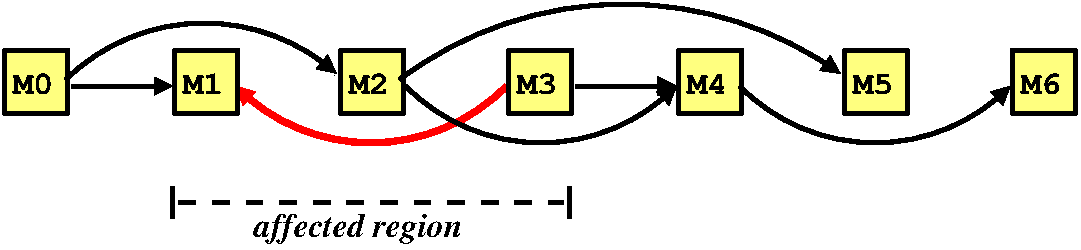
Observe, when inserting an edge Mx --> My, there is a 50% chance mutexes Mx and My are already correctly ordered and, hence, no further work is required! However, if they are incorrectly ordered (as above), then either: they do form a cycle (hence, we have detected a potential deadlock); or, they don’t and the ordering needs updating. To figure this out, we must traverse some (or all) of the graph. My algorithm improves upon the naive approach (i.e. always traversing the whole graph) by limiting the search to just the affected region. That is, those mutexes beteween the two end points of the edge being inserted (as shown above). Of course, in the worst case, the affected region is the whole graph! But, in the average case, it is often much less (as above). The key is that my algorithm never does more work than the naive approach, and usually does a lot less. For graphs with a reasonable number of vertices, this offers considerable performance improvements (hence, presumably why the Abseil developers chose it).

Conclusion

Hopefully, that’s given you an insight into the deadlock detection algorithm used in Abseil. It’s an interesting problem that turns out to be ideally suited to my algorithm, and something I had never thought of. That’s the beauty of algorithms — sometimes they have a life of their own!