Dr. David J. Pearce

Generating Verification Conditions for Whiley

Tuesday, December 4th, 2012

Probably the most interesting aspect of the Whiley language is that it supports compile-time verification of preconditions, postconditions and other invariants.  There are two main aspects of how this works:

In this article, I’ll be presenting the mechanism for generating verification conditions in the Whiley compiler, since it’s a tricky process to get right.  Also, understanding this really helps to understand what exactly the automated theorem prover does.

Understanding Verification Conditions

As a first example, consider this simple Whiley program:

 int inc(int x) requires x >= 0, ensures $ > 0:
    return x + 1

The function inc accepts a single parameter x where it is required that x >= 0 on entry (a.k.a the precondition).  The ensures clause of the function mandates that the return value (given by $) must be greater than zero (a.k.a the postcondition). The Whiley compiler must verify the postcondition holds assuming the precondition does. To do this, it generates a verification condition at the return statement with which the ATP can decide whether an error exists or (i.e. whether or not the VC is satisfiable).

For the above example, the verification condition would be: x >= 0 ==> x+1 <= 0.  Now this might seem odd if you had been expecting x >= 0 && x+1 > 0. To understand what’s going on, it’s useful to split the VC into: the assertion being checked; and, the assumptions we have.  For the above program, the assertion we’re checking is that $ > 0 which, if we substitute $ for the actual returned value, gives us x+1 > 0. The assumptions we have are that x >= 0. To construct the VC, we combine the assumptions and assertion together using ==> (i.e. an implication) to give our final verification condition.

Basic Control-Flow

We’ll now consider the process of generating verification conditions in more detail.  To begin with, we’ll just consider basic control-flow (i.e. if statements) to get the idea.  Here’s an example:

int abs(int x) ensures $ >= 0:
    if x >= 0:
         return x
    else:
         return -x

This example is nice because it only consists of an if statement along with a postcondition.  To verify this function the verifier performs a path-sensitive traversal, accumulating the verification condition as it goes.  In this case, it will first traverse down the true branch and then, separately, traverse down the false branch.  When doing this, it will assume the branch condition holds (resp. does not hold) as appropriate.  The following illustrates the process:

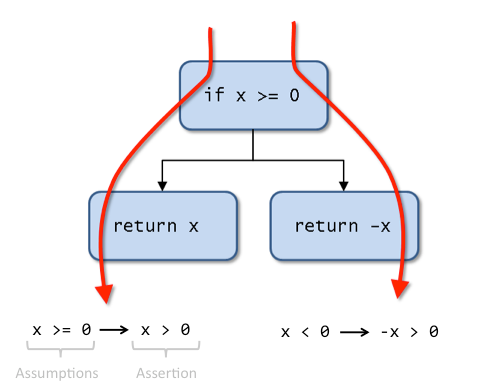
Here, we see the two execution paths that the verifier traverses along with the verification conditions generated for each.  Upon reaching a return statement, the verifier must check the postcondition holds.  This is done by first substituting $ for the returned expression to generate the assertion and combining it with the accumulated assumptions to produce a verification condition.  The verifier then passes each of these to the automated theorem prover which attempts to prove they are unsatisfiable (and, hence, that the postcondition holds for all executions of that path).

Whilst the above example is very simple, it does illustrate the main points.  A slightly more complex example is the following:

int abs(int x, int y) ensures $ >= 0
    if x < 0:
        x = -x
    if y < 0:
        y = -y
    return x + y

This takes the basic idea from before, but adds a second conditional. Since the generation process is done using a path-sensitive traversal, we end up with four distinct verification conditions to be checked. The following illustrates:

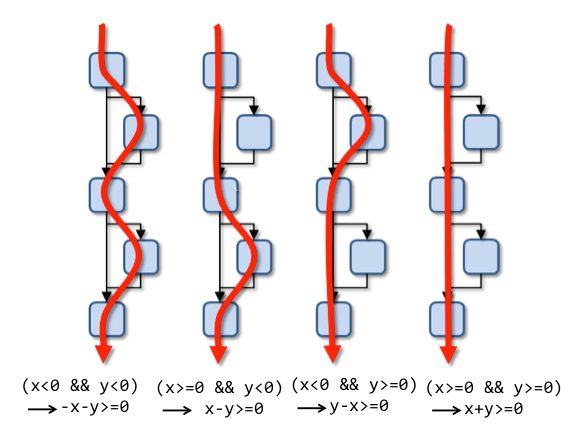
Here, we can see how the verification condition generator has propagated the effects of assignments through subsequent expressions to produce a verification condition expressed in terms of the function parameters.

Pre-/Post-Conditions

A precondition is a set of constraints that are assumed to hold on entry to a function.  The idea is to assert (i.e. check with the automated theorem prover) that a function’s precondition holds when it is called, and then assume it does within its body.  In contrast, a postcondition is asserted at all return statements within the function body and then assumed at call sites.  To help make this distinction clear, it’s useful to imagine the code has explicit assume and assert statements which capture this behaviour.  To illustrate, here’s a (recursive) implementation of Euclid’s algorithm for find the Greatest Common Divisor:

int gcd(int a, int b) requires a >= 0 && b >= 0, ensures $ >= 0:
    if b == 0
       return a
    else:
       return gcd(b, a % b)

The above is provided as-is to the VC generator, which we now imagine inserts assert and assume statements (before proceeding to actually generate VCs) like this:

int gcd(int a, int b) requires a >= 0 && b >= 0, ensures $ >= 0:
    // generated from my precondition
    assume a >= 0 && b >= 0
    //
    if b == 0
       // generated from my postcondition
       assert a >= 0
       //
       return a
    else:
       // generated from call target's precondition
       assert b >= 0 && (a % b) >= 0
       // generated from my postcondition
       assert gcd(b, a%b) >= 0
       //
       return gcd(b, a % b)

The VC generator then performs the path-sensitive traversal accumulating assumptions and, for each assert, invokes the automated theorem prover to check the condition holds.  The assume statements are assimilated into the set of assumptions when encountered and do not cause the automated theorem prover to be invoked.  The above example generates three verification conditions to be checked — i.e. one for each assert statement (in this case).  These are:

A final point about postconditions is that the VC generator must be careful to retain the original values of parameter variables.  Consider this example, where the postcondition explicitly refers to the parameter x:

int increment(int x) ensures $ > x:
    x = x + 1
    return x

To see the problem, let us naively imagine that an assert statement is inserted (like before) as follows:

int increment(int x) ensures $ > x:
    x = x + 1
    // generated naively from my postcondition
    assert x > x
    //
    return x

We can clearly see that x > x can never be true — so something must be wrong! The problem is that, in generating the assert statement, we have not used the original value of x on entry. To correctly insert an imaginary assert statement, we must insert additional code as follows:

int increment(int x) ensures $ > x:
    $x = x
    x = x + 1
    // generated sensibly from my postcondition
    assert x > $x
    //
    return x

Here, we’ve inserted an imaginary “shadow” variable (i.e. $x) to store the value that x held on entry. The VC generated is then: x+1 > x which is evidently true.

Loop Invariants

Dealing with loops is more challenging than the basic control-flow we’ve seen above.  Consider this  example:

define nat as int where $ >= 0

nat loop(nat start, nat end):
    i = start
    r = 0
    while i < end:
        r = r + i
        i = i + 1
    return r

(note: this example uses Whiley’s define statement to define a constrained type. These are treated the same as before and expand as pre-/post-conditions)

The problem with the above is that the VC generator cannot perform a true path-sensitive traversal of the function since it has an infinite number of paths. Therefore, it approximates this by traversing the loop just once. The user must provide a loop invariant to help the VC generator do this.  Adding a loop invariant to our above example looks like this:

define nat as int where $ >= 0

nat loop(nat start, nat end):
    i = start
    r = 0
    while i < end where r >= 0 && i >= 0:
        r = r + i
        i = i + 1
    return r

The VC generator must first assert the loop invariant holds on entry to the loop; then, it will assume it at the start of the loop body along with the loop condition and, from this, assert the loop invariant holds at the end of the body. We can expand the example to illustrate this by inserting assert and assume statements as before:

define nat as int where $ >= 0

nat loop(nat start, nat end):
    i = start
    r = 0
    // generated to check invariant holds on entry
    assert r >= 0 && i >= 0
    //
    while i < end where r >= 0 && i >= 0:
        // generated from my loop invariant
        assume i < end && r >= 0 && i >= 0
        //
        r = r + i
        i = i + 1
        // generated to check invariant holds on next iteration
        assert r >= 0 && i >= 0
        //
    // generated from loop condition and invariant
    assume i >= end && r >= 0 && i >= 0
    //
    return r

In the above, there are two distinct paths that the VC generator will traverse: the first goes into the loop and stops at the end of the body; the second skips the loop body entirely.  The following illustrates these two paths:

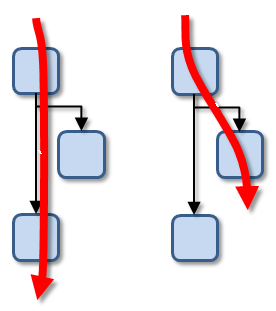
An important issue which is not clear above, is that the VC generator must invalidate variables which are modified in the loop body before each of the assume statements.  To understand this better, consider the following example:

int f(int end):
    i = 0
    r = 0
    assert r < 10
    while i < end where r < 10:
        assume r < 10
        r = r + i
        i = i + 1
        assert r < 10
    ...
    return r

If the VC generator does not invalidate the variables i and r on entry to the loop, then it will retain the initial values assigned to those variables for the single iteration of the loop it considers. When it reaches the end of the loop body, the value retained for r will be 0 and the assertion will trivially hold despite the fact that it is invalid. The invalidation of a variable is achieved by assigning it a fresh variable (i.e one which is not used elsewhere in the program code, often referred to as a skolem constant).

Consider the path taken by the VC generator through the loop body. Let’s assume variable r is invalidated on entry to the loop by assigning the skolem $r0 and variable i is invalidated by assigning $i0. Then, the resulting verification condition at the end of the loop body would be: ($r0 < 10 && $i0 < end) ==> $r0+$i0 < 10. Since this formula has many invalid assignments (e.g. $r0 == 9 && $i0 == 1 && end == 20), the automated theorem prover will now correctly identify the error present in the code.

Conclusion

Hopefully, this article helped you understand what verification conditions are, and how they are generated.  There is, unfortunately, quite a lot about generating verification conditions for modern languages (e.g. Whiley) that I’ve left out in order to keep the article focused.  In the future, I’ll expand on the more advanced issues and give insight into how things work inside the Whiley compiler.  For now, I’ve compiled a list of relevant papers which should provide useful additional background.

Further Reading

There are quite a few interesting papers and articles on the subject of generate verification conditions.  Here’s a selection of those I’ve found interesting: