A Problem with Structural Subtyping and Recusive Types

One problem causing me a headache is how to implement structural subtyping for recursive types (which I first blogged about here). The following example illustrates the basic idea:

define Link as { int data, LinkedList next }
define LinkedList as null | Link

LinkedList f(Link list):
    return list

This is a fairly straightforward definition of a linked list, along with a dumb function f() that just returns its parameter. The key here, is that for f() to type check, we must show Link to be a subtype of LinkedList. In otherwords, to show that Y < {int data, null|Y next} > is a subtype of X < null | {int data, X next} >.

Here’s a pictorial representation of the problem:

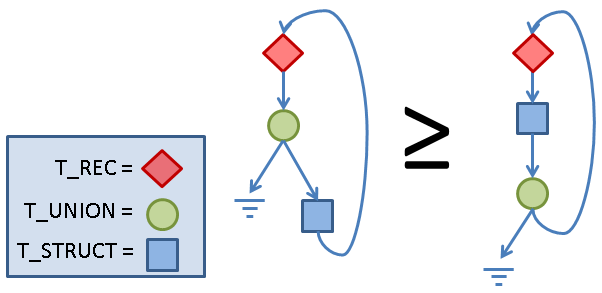
Now, the following illustrates my current (abbreviated) subtyping implementation, with each rule annotated with its corresponding name from the technical report:

define T_INT as 1
define T_NULL as 0
define T_UNION as {Type}           // a union (i.e. set) of types
define T_STRUCT as {string->Type}  // map fields to types
define T_REC as { string var, Type body } // recursive types

define Type as T_INT | T_NULL | T_REC | T_UNION | T_STRUCT

bool isSubtype(Type t1, Type t2):
 if t1 == t2:
     return true
 else if t1 ~= T_UNION:
     // rule S_UNION1
     for Type t in t1:
         if isSubtype(t,t2):
             return true
     return false
 else if t2 ~= T_UNION:
     // rule S_UNION2
     for Type t in t2:
         if isSubtype(t1,t):
             return true
     return false
 else if t1 ~= T_STRUCT && t2 ~= T_STRUCT
     && dom(t1) == dom(t2):
     // rule S_DEPTH
     for (f->t) in t1:
         if !isSubtype(t,t2[f]):
             return false
     return true
 else if t1 ~= T_REC && t2 ~= T_REC:
     // rule S_RECURSE
     return isSubtype(t1.body,t2.body)
 else if t1 ~= T_REC:
     // rule Q_UNFOLD (part of)
     t1 = unroll(t1)
     return isSubtype(t1,t2)
 else if t2 ~= T_REC:
     // rule Q_UNFOLD (part of)
     t2 = unroll(t2)
     return isSubtype(t1,t2)
 else:
     return false

The unroll() function does what you’d expect: it takes a recursive type and substitutes its body for itself. So, for example: X < null | {int data, X next} > unrolls to this: null | {int data, (X < null | {int data, X next} >) next} Unfortunately, isSubtype() will not conclude that Link is a subtype of LinkedList.  The problem is that, on entry, we have two instances of T_REC with different bodies.  Thus, isSubtype() will attempt to recursively identify whether the first body is a subtype of the second (which it is not because it ends up with the case isSubtype(X,null|X)).

Apparently, the following papers tell me how to solve this problem:

• Efficient Recursive Subtyping, Dexter Kozen, Jens Palsberg and Michael Schwartzbach.  POPL, 1993. [ACM DL] [PDF]

• Subtyping Recursive Types, Roberto M. Amadio1 Luca Cardelli, TOPLAS, 1993.  [ACM DL] [PDF]

• Efficient Inclusion Checking for Deterministic Tree Automata and DTDs, Jérôme Champavère, Rémi Gilleron, Aurélien Lemay, and Joachim Niehren, 2008. [PDF]

… I just need to figure them out first!